Crear algoritmos cuanticos

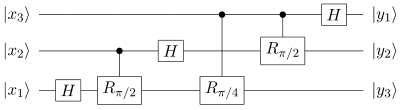
Un algoritmo cuántico es un algoritmo que se ejecuta en un modelo realista de computación cuántica, como el modelo de circuito cuántico, como el que se ilustra en la figura.1​ La teoría de la complejidad computacional le asigna la clase BQP a los algoritmos que pueden ser resueltos en un computador cuántico en tiempo polinómico con un margen de error promedio inferior a 1/4. En el análisis de los algoritmos cuánticos es habitual comparar la cota superior asintótica con el mejor algoritmo clásico conocido, o, si el problema está resuelto, con el mejor algoritmo clásico posible.

Se usa la notación de Landau para definir la relación entre la talla de la entrada del problema y el número de pasos necesarios para resolverlo, o el número de posiciones de memoria que se utilizan durante su resolución.

El objetivo de este articulo es presentar una introducción a los principales algoritmos cuánticos y en concreto:

• 1. Entender cómo el paralelismo cuántico se puede usar para realizar cálculos de forma más eficiente.

• 2. Ser capaz de describir circuitos cuánticos para la resolución de los problemas de Deustch, Deutsch-Jozsa y Simon.

• 3. Conocer el algoritmo de Grover y analizar su complejidad.

• 4. Conocer el algoritmo de Shor y analizar su complejidad.

Un algoritmo es un proceso encaminado a realizar una tarea específica.

Cada etapa de un algoritmo cuántico se especifica mediante una puerta cuántica, que no es otra cosa que una transformación unitaria en el espacio de Hilbert. Por tanto, el algoritmo se expresa mediante composición de transformaciones unitarias y en consecuencia siempre es reversible, porque toda transformación unitaria tiene inversa.

Representaremos los algoritmos mediante circuitos, que evolucionan de izquierda a derecha, en los que se representan las distintas puertas cuánticas usando los símbolos introducidos

Para seguir adecuadamente la evolución del estado a lo largo del circuito hay que recordar que:

La medida del primer qubit del estado de salida se hace con la base B1. Si el resultado de la medida es 0 la función es contante y si es 1 no lo es.

Aunque generalmente los algoritmos cuánticos son probabilísticos, en este caso se obtiene un algoritmo determinista para resolver el problema, ya que se consigue la solución con probabilidad 1. Por tratarse de un problema de complejidad constante, no podemos sacar ninguna conclusión al compararlo con los algoritmos clásicos.

El problema de Simon fue una de las primeras cuestiones que se resolvieron en computación cuántica con ganancia exponencial. Clásicamente, para resolver el problema es necesario evaluar f sobre la mitad más 1 de los elementos del dominio. Es decir, 2(n-1)+ 1 evaluaciones. Si queremos la solución con una probabilidad de error menor que ε, se puede conseguir con 2(n-1)/2 (1-ε)1/2 evaluaciones. Cuánticamente el problema se puede resolver con O(n-1) evaluaciones.

Problema de Simon:

Determinar, con el mínimo número posible de evaluaciones, el periodo de una función f de (Z2)n en (Z2)n, periódica y 2 a 1.

Definiciones: (Z2)n es el espacio vectorial de las cadenas de n bits (con la suma módulo 2 bit a bit). Se dice que una función f de (Z2)n en (Z2)n es periódica de periodo T (donde T es una cadena de n bits) si para toda cadena k se verifica que f(T+k)=f(k) y se dice que es 2 a 1 si para toda cadena h de la imagen de f hay dos cadenas k1 y k2 tales que f(k1)=f(k2)=h.

Algoritmo cuántico para el problema de Simon:1. Inicializar el 2n-qubit |0>|0>
2. Aplicar Wn a los n primeros qubits
3. Aplicar Uf
4. Medir los n últimos qubits (resultado j=j1 ... jn)
5. Aplicar de nuevo Wn a los n primeros qubits
6. Medir los n primeros qubits. Devolver el resultado k=k1 ... kn

El resultado final es un entero k (cadena de n bits) de modo que k·T=0.

Veamos la evolución del algoritmo:

La primera medida da como resultado cualquier valor de la imagen de f con probabilidad 1/2(n-1), por ser una función 2 a 1, y la segunda cualquier valor k, que cumple T·k=0, también con probabilidad 1/2(n-1).